My, my, how naughty have I been. I will not dwell on the fact that it has been a while since I was supposed to write this, and we shall continue very quickly. I have also acquired an epic thing for these posts, that being KaTeX, which should allow me to input png’s of equations. This will hopefully be easier to read than last time.
I would like to start off with some more basic concepts that are essential if you want to do something in this space. The following is the plan:
- Subgroups
- Cosets
- Conjugation
- Normal Subgroups
- Conjugacy Classes
- Quotients
- Direct Products
- Progress on my result
Subgroups
Subgroups are fairly simple to comprehend. If you take a set of elements in a group G, and these elements form a group under the group operation of G, then that set is a subgroup. We can take an example from the dihedral groups. Let’s take D4. This group has a couple of subgroups. One of them is the subgroup generated by the rotation r. This subgroup (which let’s denote as H1) is the following.
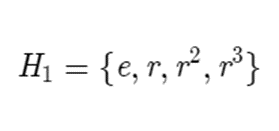
We can check that this subgroup satisfies the properties of a group. This set is closed, since multiplying rotations isn’t going to give you anything other than another rotation. All of these elements have to be associative since they’re all part of the group D4. The identity is the rotation of 0 degrees, and the inverse of any rotation is also going to be a rotation, so it will be included in the set H1. Thus H1 is a group.
There are other subgroups such as the following.
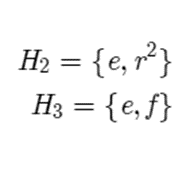
Where H2 is the subgroup of all even powers of r, and H3 is the subgroup generated the flip f. Generally, if you have a subgroup H in G, then we denote that with
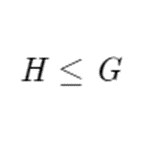
Note that under this definition, every group has at least two subgroups. The first being the group itself, and the second being the trivial subgroup containing only the identity. That first subgroup isn’t very useful for many things and falls under this definition out of necessity. If your subgroup H in G doesn’t equal G, then we say that H is a proper subgroup, denoted as
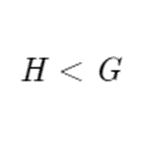
Cosets
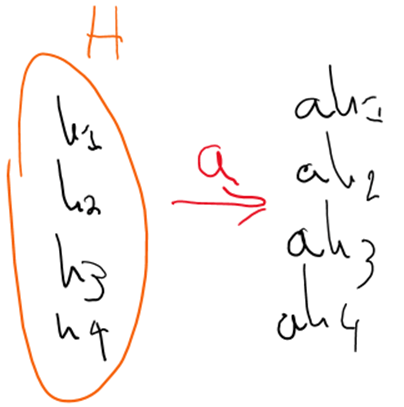
An interesting thing we can do with subgroups is make cosets out of them. You make a coset out of a subgroup H by multiplying every element of H by an element in G, which we’ll call a. Here, a is called the representative, and the coset of H multiplied by a is denoted with aH, and contains the following elements.
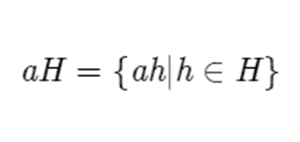
Or in other words, all elements of H multiplied by the representative a.
It is very important to note that there exist two types of cosets: left ones and right ones. This arises from our definition, where to make a coset, you multiply its elements by a representative. However, we never specified what side we were multiplying the elements of the subgroup from. This is important, since commutativity isn’t a prerequisite for a group, and thus ah isn’t the same as ha. We reconcile this difference by defining a left coset aH, and a right coset Ha as the following.
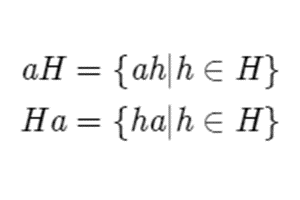
Note that cosets are not subgroups, only paper copies of the subgroup in G, as they will lose the identity element, and thus cannot be a group.
Another important property of subgroups is that if you choose a representative in a coset, then forming another coset (left or right) using that representative will create the same coset. We can prove this by trying to make a new coset using an element in aH.
Take an element in aH which we will call b, and an arbitrary element in aH, which we will call h.
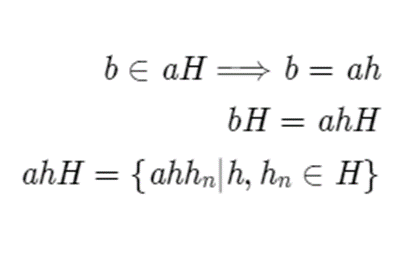
Given that both h and hn are elements of H, we know that their product is also in H, since H is a group, which is closed by definition. Thus
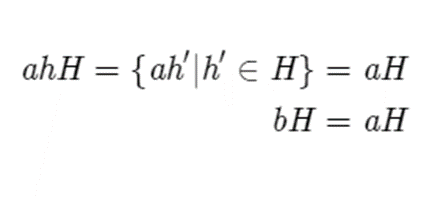
Which proves that trying to generate a coset using an element already in a coset will not yield anything new. Even further than this, you can prove that if cosets are not identical, then they are completely disjoint (meaning they don’t share any elements in common). This means that you can completely express the elements of a group G using only cosets, since any element not already in a coset will have to generate a new coset which is guaranteed to be different from every other coset. When this happens, we say that the cosets partition G.
To wrap the explanation of cosets, let’s look at an example. Again, take the group D4. One of the subgroups in D4 is the group generated by the flip, or H = {e, f}. The cosets of H in D4 are these.
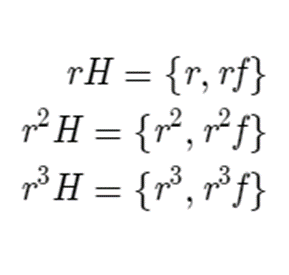
You can see from a visual representation that these cosets represent copies of the subgroup in the group.
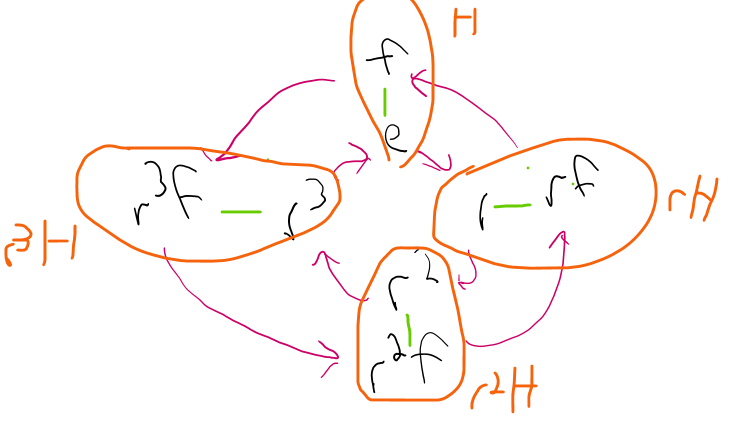
It should be clear from this example that the order of a group (the size, or the number of elements in the group) is a multiple of the order of one of its subgroups. Or more usefully, the order of a subgroup must be a factor of its parent group. This comes simply from the fact that the subgroup partitions G, so G is made from some whole number multiple of them. This result is known as Lagrange’s theorem, and it severely limits the number of subgroups that a group can have.
Let it be known that the number of copies of a subgroup H in G is called the index of H in G. This can be thought of as the number of times H goes into G, written like this.
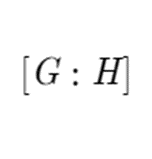
The index allows us to precisely write Lagrange’s theorem as so.
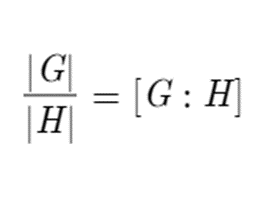
Conjugation
I would like to define a useful operation before we continue. This operation is called conjugation. When we have two elements in a group, a and b, we say that the conjugate of a by b is the following.
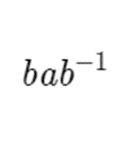
Conjugation will have more to offer us soon, but it’s good set up for the next section.
Normal Subgroups
The difference between left cosets and right cosets can be a tricky thing to keep track off. Though they usually behave the same way (and it won’t matter which one you use most of the time), they are not the same, and you need to be careful not to interchange them. However, there are some cases where the left and right cosets of a subgroup are the same. When this happens, we call that subgroup normal in G, represented by this symbol.
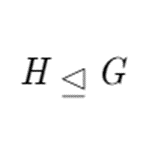
As with regular subgroups, this permits G itself to be a normal subgroup. When this isn’t the case, you say that H is a proper normal subgroup of G, written as
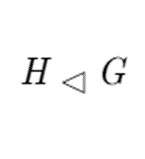
We can come up with an alternate definition of normal subgroups using conjugation by a simple process. If we take the definition of a normal subgroup, we can do a nice algebraic step and get an interesting relation.
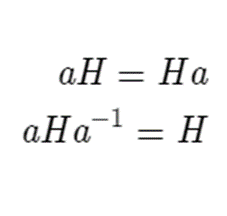
So we now have two definitions for a normal subgroup, one where left cosets equal right cosets, and another where the conjugates of every element in the subgroup is also in the subgroup. That second definition makes normal subgroups quite useful, as it allows you to simply a lot of algebra.
Conjugacy Classes
We will return to conjugation, as it brings some interesting properties with it. The first thing we are going to notice is that conjugacy is an equivalence relation. For this to be true, it must have the three properties of an equivalence relation.
Reflexive : a must be equivalent to a. In the case of conjugacy, this means that we need to be able to conjugate an element a by some other element, and return a. This can be done easily by conjugating a by the identity.
Symmetric : If a is equivalent to b, then b must be equivalent to a. We can show that this holds for conjugacy by the following.
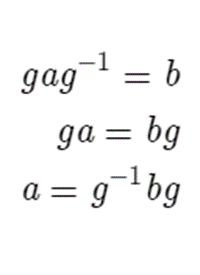
Thus if b is a conjugate of a, then a is a conjugate of b.
Transitive : If a is equivalent to b, and b is equivalent to c, then a must be equivalent to c.
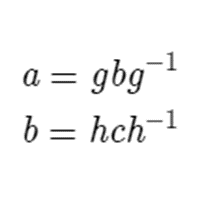
Substituting b with hch-1 gives
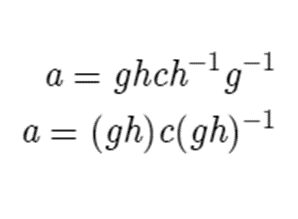
Which shows that a is a conjugate of c by gh.
With all three properties satisfied, we have proven that conjugacy is an equivalence relation. A nice consequence of this is that this provides us with equivalence classes, called conjugacy classes in this case. More specifically, the conjugacy class of an element a in G contains all the possible conjugates of a in G, or taking a and conjugating by every other element in G, the ensuing set is the conjugacy class of a, written
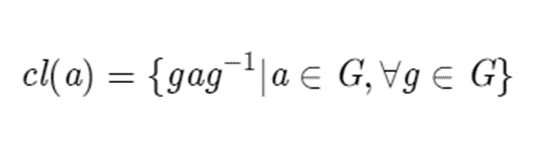
Not only does this set contain every conjugate of a, but every element in cl(a) will have the same conjugacy class of a, since it is an equivalence relation. The conjugacy classes of G also partition G, since any element not already in a conjugacy class, is going to generate a new conjugacy class, and no overlap can occur, since this would imply that both conjugacy classes are the same.
From this fact, we can make something called the class equation, which is just another way to represent a group, except this time using its conjugacy classes.
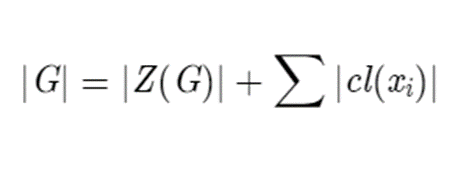
Where cl(xi) are all the distinct conjugacy classes of order larger than one, and Z(G) is the centre of G, which contains the elements in G that are commutative with every other element. This is relevant since the conjugacy class of an element, z, in the centre of the group is going to be the set containing only z.
The final property of conjugacy classes we’ll talk about, is that elements in the same conjugacy class have the same order. If we have an element x and its conjugate gxg-1, and we assume that |x| = n, then we have the following.
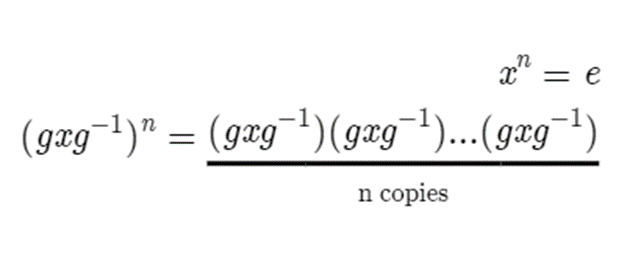
If we get rid of the brackets, then we see that all the interior g-1’s and g’s cancel out, leaving
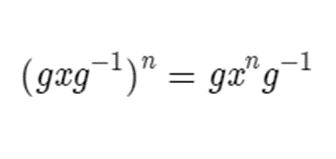
Since xn = e, we get
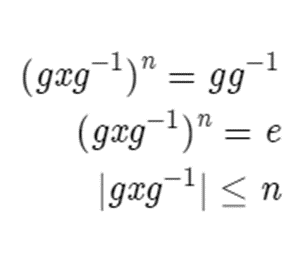
We don’t know if the order of gxg-1 necessarily equals n yet, since an element can be exponentiated by many different numbers and equal the identity. To prove that it does equal n, we can prove the inverse inequality, but that is essentially the same proof in a different direction, so I won’t do it here.
Quotient Groups
The process of taking the quotient forms smaller groups using subgroups. These were presented to me in a very vague fashion, but they essentially see if the cosets of a subgroup form a group. If it does, then it forms a quotient group. The quotient group of a subgroup H in G is written
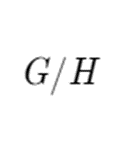
And is sometimes pronounced as “G mod H”.
It might be useful to look at an example, so let’s take the group D4 again. In this case, we want to quotient out by the subgroup
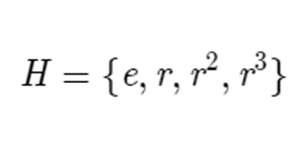
To visually interpret this, let’s see the Cayley graph of H in D4. The subgroup H is the inner ring, while its only coset fH is the outer ring. If we condense H and fH into singular nodes, we get the following series of Cayley graphs.
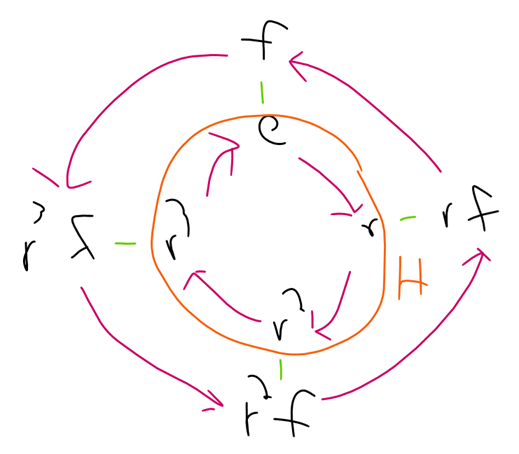
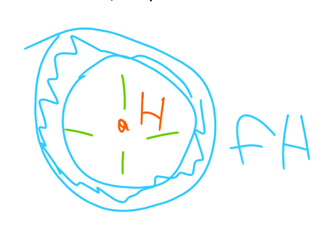


We can see that after condensing the cosets into singular nodes, and then combining redundant vertices, we get a group of order two, of which there is only one, namely C2. This means that G mod H is the same as C2, or the following
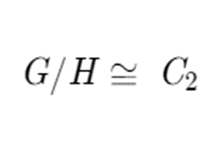
Where that funky equals sign is a special equality symbol, who’s specifics we don’t need to worry about.
This is visually what the quotient process is doing. It’s condensing cosets into nodes, which produces another Cayley graph. It is important to note that you can’t always make a quotient group. Only when this resultant Cayley graph is also a group, does the quotient group exist. So the next natural question is what the requirements are for the quotient group to exist.
The quotient group only exists when all of the vertices of a condensed node point in the same direction. Since then, they can be combined (as they are redundant) and you get a valid Cayley graph. If the vertices go in different directions, they can’t be combined, which insinuates that multiplying this condensed node (an element in the quotient) by a certain element will give two possible results, which groups cannot do (this is implicitly required in our definition of a group). But what does this mean in a more concrete algebraic sense?
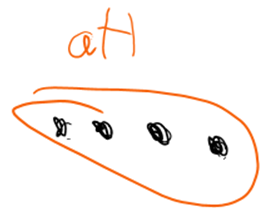
To answer this, we will take a closer look at left and right cosets and will give them visual interpretations. The left coset aH can be thought of as starting with the element a, and multiplying by each individual element of H. The resulting set of elements then form the left coset of H. This method of starting with a and multiplying by H is conveyed graphically below.

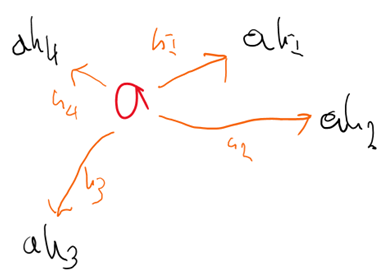
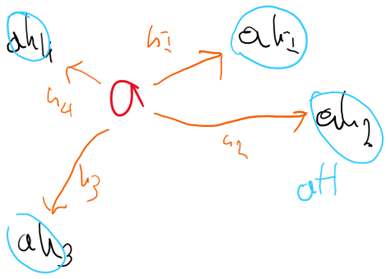
The interpretation of right cosets is the other way around, instead we starting with H and multiplying by a as below.
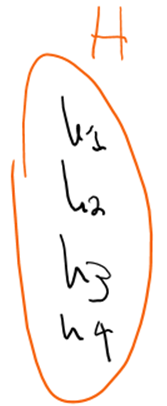
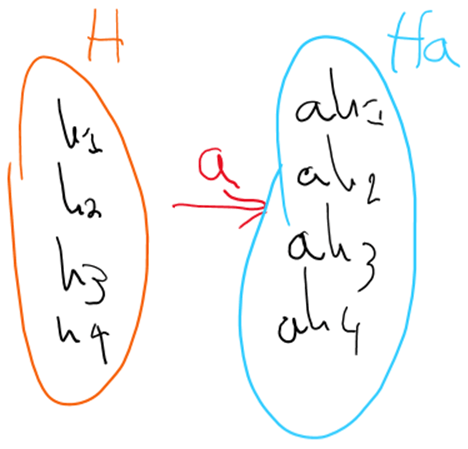
Now let’s study what happens when we take the quotient. Let’s start with a left coset and take the right coset of it. We are assuming here that left and right cosets aren’t the same, and so this isn’t a normal subgroup.
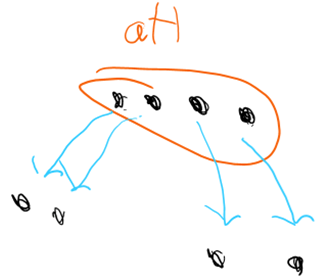
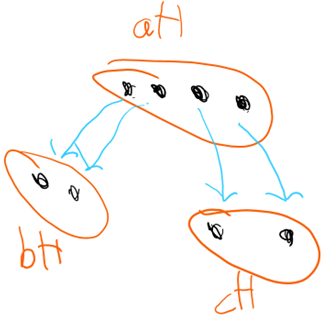

Because of the split that happened in the third step, the product of aH and the blue arrow is ambiguous, which isn’t allowed in our definition of a group, thus this quotient can’t exist. The important bit here, is that the quotient couldn’t be completed because of the split of aH that happened in step three, and this split was caused by our assumption that the left cosets don’t equal the right cosets. So that assumption of the non-equivalence of cosets caused the quotient process to not work, so it must be the case that quotients can be taken if and only if the subgroup is normal in G, and in fact, that is the criteria for the quotient to exist.
As far as I am aware, there is no useful algorithm to determine what the quotient of two groups is or what it should be, so you sort of just need to feel it out by hand if you want to find the quotient.
Direct Products
Direct products are less of a hassle. Instead of making big groups small, they make small groups big by adjoining two groups, and they do this in a very intuitive manner. The direct product of two groups A and B is the following.
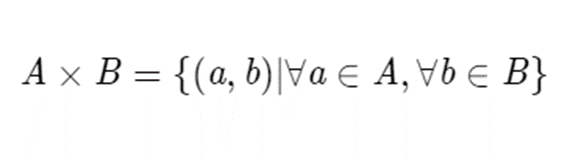
It is the group of ordered pairs, where one coordinate is from one group, and the other coordinate is from the other group. If you want to combine two elements in the direct product G, you do it component-wise. That is, the first coordinate will only every affect the first coordinate, the second coordinate will only affect second coordinate, etc. Algebraically, this is
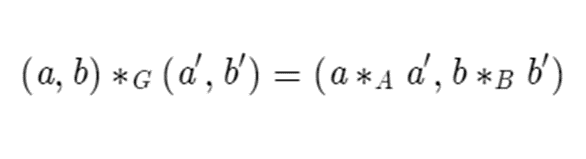
Where *G is the group operation of G which we are defining, *A is the group operation of A, and *B is the group operation of B.
Conveniently enough, the direct product of A and B mod either A or B exists and returns the other group, or
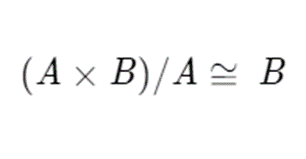
We can prove this with the following, where alpha and beta are elements of A and B respectively.
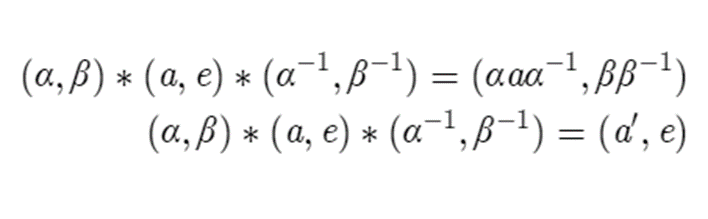
This shows that the group A is certainly normal in G, and thus G mod A will exist. We can unprofessionally determine that it will be B, since all cosets of (a’, e) will leave a’ unchanged, and only interact with e. Since only elements of B will interact with e, the cosets form the group B.
The inverse of this is not necessarily true. That is the direct product of A mod B and B is not A, or
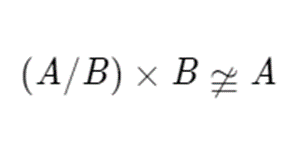
Note that the direct product can be taken with any whole number of groups as follows.
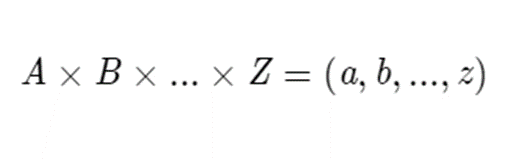
In general, the properties of the direct product don’t change no matter how many groups are involved.
Progress Delivery
I have made substantial and very good progress in my result. In my first log, I identified two main areas where my result could come from, that being Lie groups and Representation Theory. I will outline my progress in these two areas and inform you of a new third.
I learnt much about Lie groups during my last visit with my mentor, where we went on a brief discussion on them before we ran out of time. One of the stranger things that I got form that experience was the type of Lie groups that were being talked about. First of all, the definition of a Lie group didn’t seem to have many glaring subtleties, and it really was what it sounded like: infinitely big groups with infinitesimal elements, though my mentor did describe them with an interesting phraseology. He said that a Lie group was a group where you could get to any other element starting with the identity and slowly changing some sort of parameter. As far as I understand, this doesn’t seem too foreign. For example, let’s see the rotational symmetries of a circle (which I’m pretty sure actually is a Lie group). You can represent any element as the following.
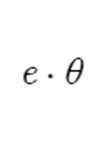
Where theta is a real number degree rotation. Slowly increasing the real number value will reach every element in the group.
The other interesting thing was the sorts of groups that were talked about. It seems that the groups I was thinking about (rotations of a circle and sphere) actually are Lie groups. Or rather, they are the same (isomorphic) to the groups they talked about. They were talking about rotations of 2- and 3-dimensional space, which are the same as my shape rotations respectively. The only major difference was that their definition of those groups was more formal, clever, and probably obvious if you have the experience. Essentially, instead of having the rotations be degree rotations, they were rotation matrices. For some reason, they also had complex variants of those space rotating groups that acted on the complex plane instead of Rn.
The most baffling part, however, was that these were the only Lie groups that were talked about. Even though we were learning about the Standard Model, the most accurate physical theory available, the Lie groups involved were just those rotations of n-dimensional space. Maybe that’s because my mentor didn’t want to discuss the more complicated Lie groups in theory, but I don’t know. More than anything, I’m curious as to what other Lie groups exist out there, but I’ll probably find my result elsewhere.
In terms of the groups-as-transformation-matrices side of things, it hasn’t been very productive. I have seen some alternate definitions and interesting tools, but nothing particularly perspective changing. Some examples include the external semidirect product, where there’s a mapping phi that sends elements of the group to an automorphism, which then permutes the elements of a complement group. There is also the wreath product, which for the life of me I can never remember the definition, but it was something like an extended external semidirect product that was permuting a big direct product. I also came across an alternative way to think of all groups as permutations. Instead of thinking about changing a shape, think of a set containing all the elements of a group, then each element in the group acts on the set by left or right multiplication, changing it into another element, thereby permuting the set via group actions. Overall, I am not too excited about getting a result from here either.
Last but not least, I came across another possible topic to work on. While reading Adventures in Group Theory by Joyner, they offhandedly mentioned something called the derived series of a group, where you continuously take the commutator subgroup of a group, and if it eventually arrives at the trivial group {e}, then the group is considered solvable. I was quickly intrigued that the mathematical community had decided to put such an important word as solvable to this weird, obscure-seeming process, as I could scarcely parse how this would make a group “solvable” at all. This definition is apparently rooted in Galois theory (get it?). I will probably pursue this as my main possible source for my result for the time being, probably starting out by trying to find the criteria for which a group is solvable.
Generally, my progress in group theory has started to speed up as I’ve become more interested in my result, and I’ve started to learn Galois theory directly.
Join me next time to probably talk about mappings and transformations, where we will go over homomorphisms, isomorphisms, automorphisms, and their fundamental theorems. I might even talk about the menagerie of interesting subgroups that can be found in this field of study.