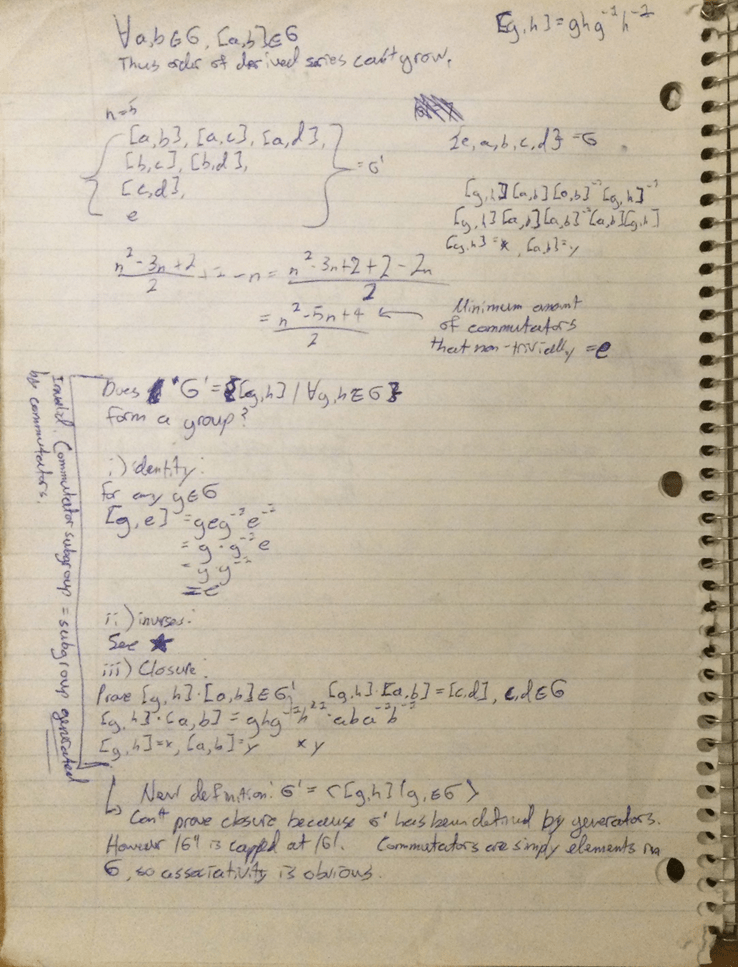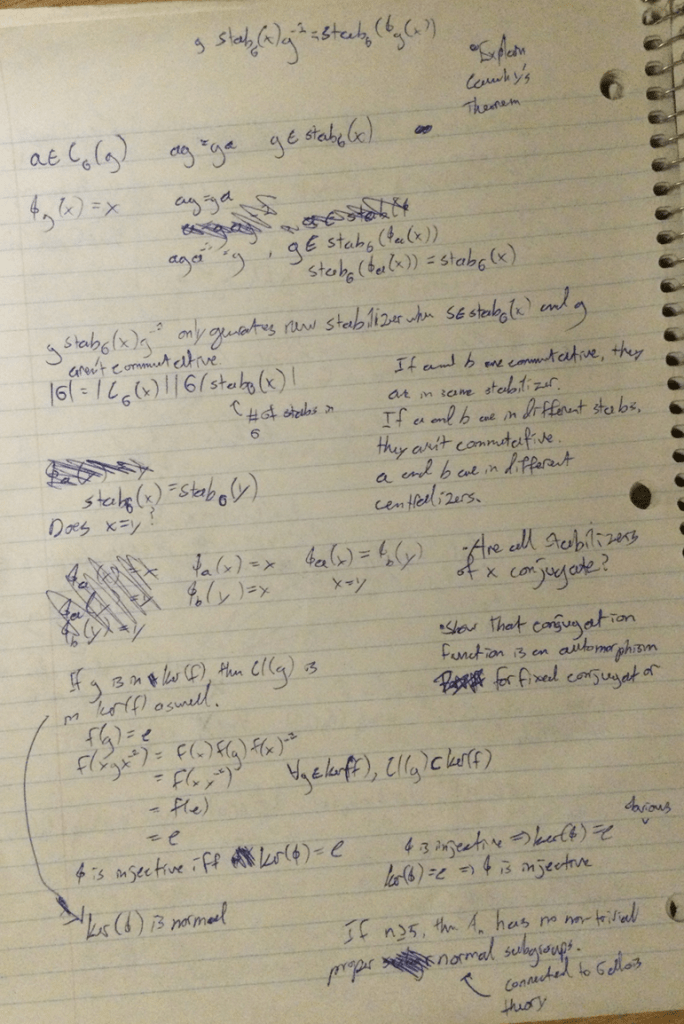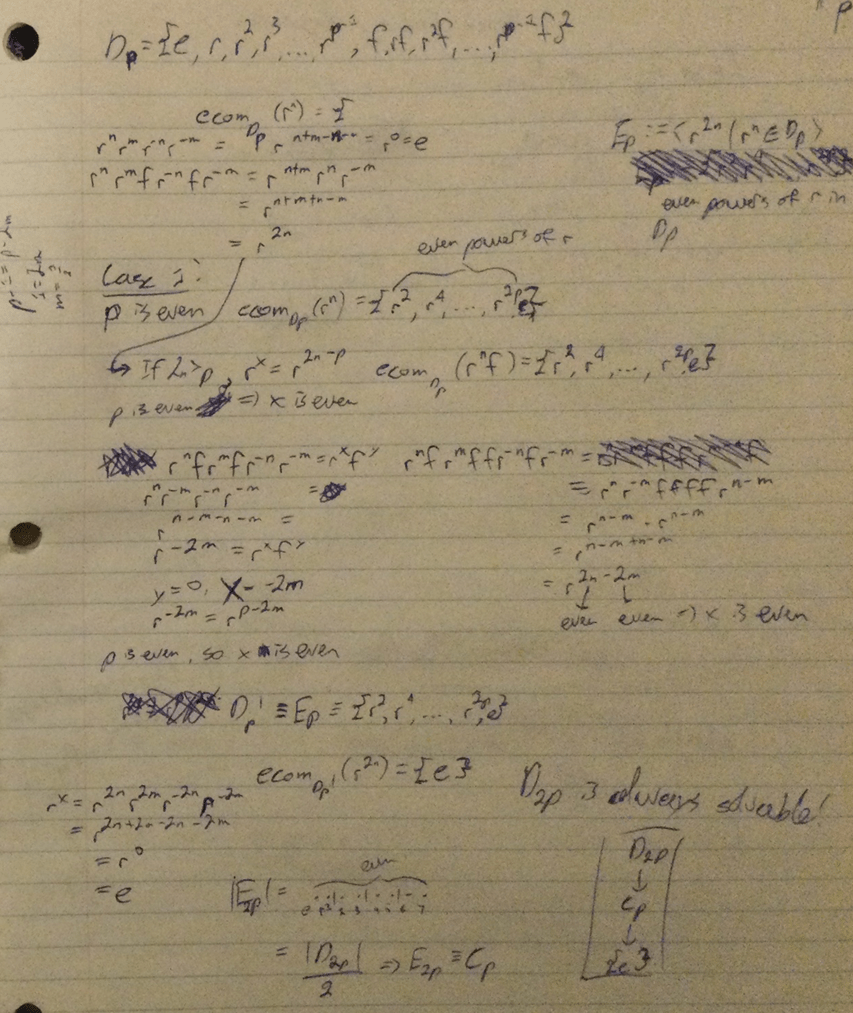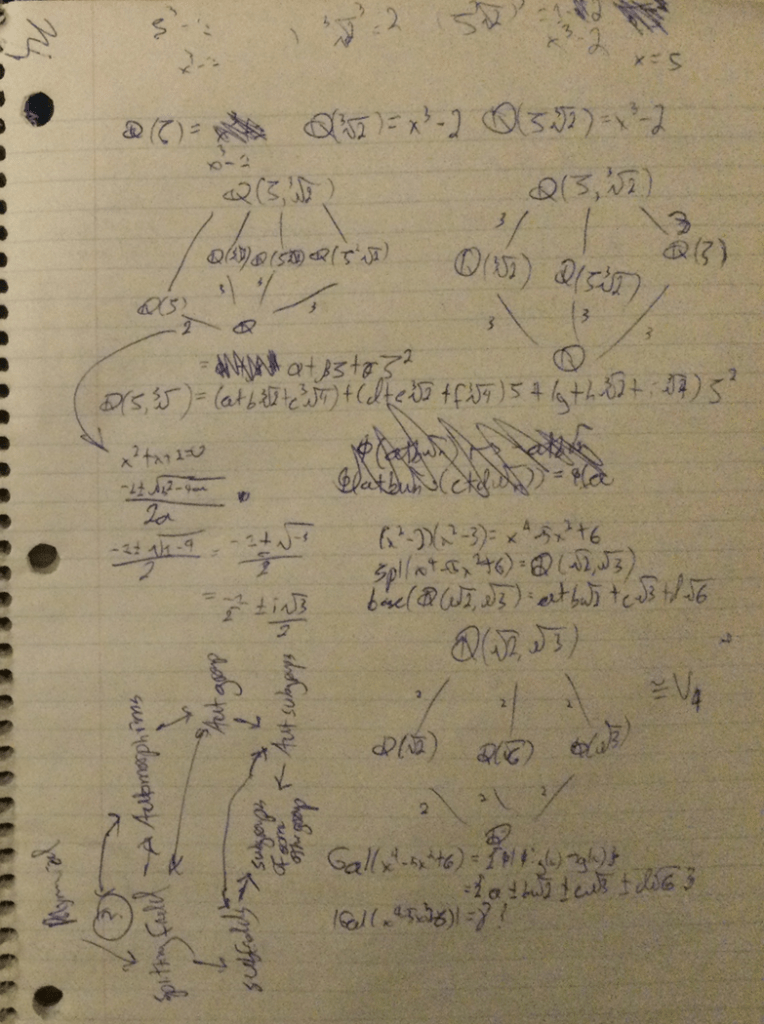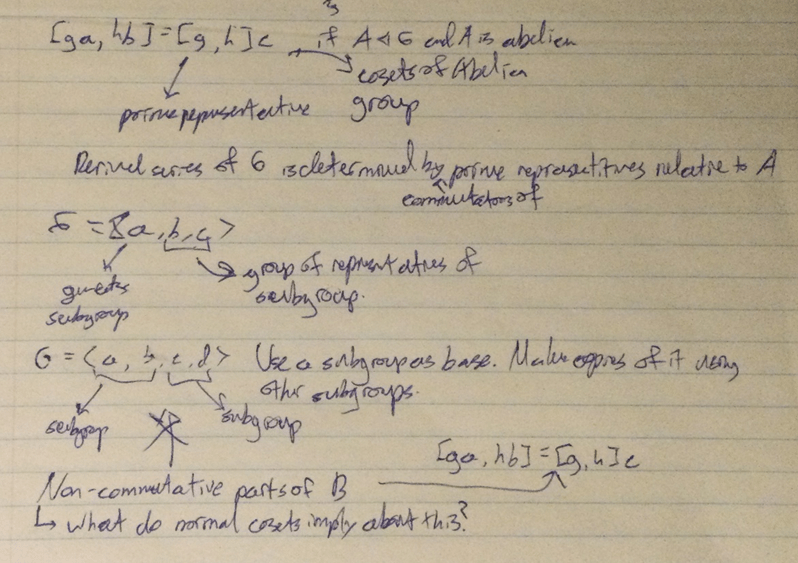Learning Opportunities
My mentor has, in fact, exposed me to new learning opportunities. Most of the stuff that I’m learning is relatively esoteric and theoretical, so the work that I do while learning remains the same across the opportunities given. Namely, solo pencil and paper work, and contemplation. Regardless, it was my mentor that referred me to the main source of information that I’ve been using throughout this whole project (Macauley lecture series). We have also peeked around his algebra and physics textbooks, which have given me glimpses of how he does math in his world of post-university. He has also provided new learning opportunities by introducing me to interesting topics to pursue while researching. For example, I never would’ve gained the understanding I have now of Lie groups had it not been for my mentor, nor would certain avenues of my result be without him either.
In terms of reinforcing new learning, there are two main systems. The first are the very exciting homework assignments. I don’t do these too often, but Macauley does provide a couple questions on his website for each section of the lecture series. I find these problems largely obtuse, in the way that it’s finding the normalizer of subgroup S in G, or the centralizer, or calculating the derived series. They are trivial exercises that exist solely to give the reader experience and familiarity, which gets boring quickly. However, familiarity with a subject can also be gained by playing around in the field, and this is our second system. This is to incorporate some of the skills I learn into my result. With this, I can smash concepts together and see what happens, perhaps giving a better understanding of how they work, while at the same time gaining practice with manipulating them. An example could be after I learned the basics for Galois theory, and I was trying to figure out the connection between Galois groups and fields. As I had recently learned about isomorphism and homomorphism theorems, I tried unraveling the connection between groups and fields by seeing if they satisfied those theorems, and thus would be isomorphic. This method quickly led to a dead end, but it was a valiant effort.
I could probably accelerate my learning by doing more of the homeworks. They’d probably do a good job of ironing out small crinkles in my understanding. I could also do more cross referencing than I currently am. I have a large collection of possible resources that I could be learning the subject from, but I’ve only used two or three.
Recollections of Mentorship
When we get together, we talk about things I’ve had trouble understanding on my own, and interesting topics that would generally be beyond my or this project’s scope. We’ve come to the conclusion that the latter might be a much more valuable use of our time together, and I can certainly say it’s very enjoyable. I’ve elaborated much in previous Log and blog posts, but we’ve talked quite a bit on Lie groups and Representation theory. These discussions were helpful in developing my result, though I’ve abandoned that path in favour of a different one. Among that, I also ask him to explain theorems I don’t understand, like the correspondence theorem, or Cauchy’s theorem.
What is going particularly well is the flow of information during our meetings. My mentor is an illuminating expositor, and it always feels like I walk out of our meetings with a new appreciation or basic understanding of some esoteric topic, which is a feeling satisfying beyond description. As much as the professional information flows, our personal information could use some work. I have learnt little about him and vice versa in comparison to the technical topics we discuss. I get glimpses occasionally, such as his dad working in the railroad industry and his feelings about complex numbers. In general, though, it’s mostly tacit. Something like the great care he takes when writing down our eclectic thoughts I find peculiar in comparison to my scribbles. This value of consistency and legibility is something I imagine he gained in university.
General Progress Report
I have finally entered into the pearly halls of Galois theory. It started out with basics on fields and representing the solutions to polynomials using fields. They then talked about subfield lattices, and how they’re the same as the group of field automorphisms. This connection hasn’t been made rigorously yet, but is a very exciting prospect. I suspect that if you could find out the connection between that Galois group and the subfield lattice, you could gain great insight into the solvability of quintics. This is what I anticipate to be coming in future lectures. Overall, I have been very excited recently, as I finally get to apply these abstract tools I’ve been developing to a real, important question.
In terms of my result, I have something which is presentable. I haven’t reached my highest standard (which would be developing the basis for a field of study like Lie groups or Representation theory), but I have something which I can be satisfied with. I might as well spoil the surprise. I have a proof that all of the dihedral groups are solvable. More generally, that any group with an abelian subgroup of index two is solvable. I don’t know how this relates to Galois theory (as it apparently does), but I know this is true. I’ve recently been trying to expand these criteria further by adding a criterion of normalcy, and I have hopes of reaching a more general result before I have to present it at In-Depth Night. The proof itself is very simple and it is nothing to be proud of, but it is something.
At this point, I only need to finish work on my result, go through the rest of the Macauley lectures on Galois theory, and then make a presentation for the Night. I will likely skip the last section of Macauley’s lectures, as they seem to talk exclusively about rings, which are a special type of group that I’m not particularly interested in for this project.
The following is a couple of pages from my notebook, where I have been fleshing out my result and understanding of certain ideas.