Come one, come all. This is the first in a series of logs (not blogs) on my In-Depth group theory project. I have mainly two goals with these entries that separate them from the required blog posts. First, I want to go through and explain some of the things that I’ve learned with a level of detail perhaps not appropriate for the blogs. This is in preparation for my final project, where I will make a lesson on some topic of my choosing. Hopefully these logs acclimate you, reader, and hone my pedagogical skills. Second, I want to give regular accounts of my result. If you didn’t know, my stretch goal is to self-derive some result in group theory. I don’t expect it to be original, but as long as I got that result without anyone teaching me, then it’s fair game. Examples include behaviours of groups, methods for dealing with them, or a proof for something. For the first couple months, this result has been ancillary to the original project, but I’ve still been gradually thinking about it, and I’d think it’d be interesting to share my process. We have ground to cover, so it’d be best to start immediately.
1.1 Lesson, Some Groups
One of the reasons this log series has taken so long to come out is that I didn’t think I had a lot of material to cover. The first chunk of my journey in group theory has largely been notation grinding. Nothing that’s hard to understand conceptually, but just getting introduced to the different way things are written, basic concepts, and other formal things. It was only this week when I was thinking about how to write this, that I realized that without covering the formalities, my explanation seemed like gibberish. Glossing over way too many things to give the reader any sense of understanding. So I’ll introduce the formalities as we need them.
I want to go through some basic groups for this first lesson, which will hopefully give you a good feel for what a group is. With that foundation, we will then talk about quotient groups in the next log.
The groups covered here:
- Abelian groups
- Dihedral groups
- Cyclic groups
- Symmetric groups
1.2 Group Definition
Yeah. This is when I realized I had actually done a lot for this project: when I realized the reader didn’t know what a group was yet.
Fundamentally, groups are pretty simple. All they really are is a binary operation and a collection of things which satisfy four properties under that operation. A binary operation is an operation that takes two inputs and gives one output. For example, addition is a binary operation. You take two numbers, add them together, and get one number. Other binary operations include subtraction, multiplication, and division, among others. So the group’s operation gives the things in the group a way to interact with each other, granted they satisfy these four properties:
Closure : If I take two things in the group (elements) and combine them using the operation, then the result must also be part of the group. I.e., combining elements in the group will never take you outside the group; it is closed.
Identity Element : There should be one element in the group that, when combined with any other element in the group, gives back that secondary element unchanged. This is called the identity and is often denoted with e, 1, or 0 (we will use e). For example, the identity element for addition is 0, because any integer plus 0 leaves that integer unchanged. Other identities are 1 under multiplication, and 360° under rotation. It is important to note that there is only one identity in a group, and this identity must work for all elements.
Inverses : For any element in the group, there is some other element in the group that, when the two are combined, give the identity. Algebraically, for every element a in the group, there is some other element a-1 in the group such that a ∙ a-1 = e. For the integers under addition, their negative counterpart is their inverse (e.g. 5 and -5, 7 and -7, etc.). Note that there are many inverses in a group, as every element has a unique inverse, otherwise they’d be the same element:
a ∙ a-1 = b ∙ a-1
a ∙ a-1 ∙ a = b ∙ a-1 ∙ a
a ∙ e = b ∙ e
a = b
Associativity : This is less alien of a concept. The operation needs to be associative. I.e., it doesn’t matter where you put the brackets when combining elements.
Every element in the group must satisfy these properties under the operation. If even one element in your collection doesn’t meet one of these requirements, then the collection isn’t a group.
There are a couple things which are important to note. First, a group is a set of elements and an operation. The integers do not form a group, but the integers under addition do; the group doesn’t exist if there isn’t an operation. Second, the identity element (the “do nothing” action) is always a part of the group. Third, groups only need to be associative under the operation, not commutative.
Lastly, as a notation thing, when talking about a group whose operation is unknown or purposefully general, the operation is referred to as multiplication, though it might not be the multiplication that you’re familiar with on the real numbers. Consequently, combining elements is written using the multiplication symbol ∙ though it can be omitted just as with real number multiplication:
a ∙ b ∙ c = abc
1.3 Abelian Groups
Phew. That might be a lot to take in, but I assure you it’s simple under the hood, and you’ll probably get the hang of it after enough exposure. So let’s give some of that exposure and start talking about some basic groups.
The first type of group on the list are abelian groups. The definition of an abelian group is pretty simple. It satisfies all the general properties of a group given above, with one extra. You will recall that I said commutativity isn’t a requisite for a group, but doesn’t mean that groups can’t be commutative. Groups that are commutative are called abelian groups.
Unfortunately, I don’t know a whole lot about abelian groups, and according to my mentor, they are largely uninteresting, with all the action happening in non-abelian groups. However, it’s still useful to know what they are.
1.4 Dihedral Groups
Swiftly moving on, dihedral groups are much more interesting, and I’d like to introduce some new concepts using them. But first, what is a Dihedral group?
A dihedral group is the group of symmetries of a regular n-gon. Let’s unpack what that means. An n-gon is any 2-dimensional shape with n sides, and regular means that all the side lengths and internal angles are the same. For example, Fig. 1.4.1 is certainly a 4-gon; it has four sides. However, it is not regular. The angles are not the same, and the side lengths are not the same. On the other hand, Fig. 1.4.2 shows what the regular 4-gon looks like – it’s a square. And the next couple regular n-gons are shapes you’re familiar with: triangles, pentagons, hexagons, etc.


So what do I mean by symmetries? A symmetry of a shape is any action that leaves its imprint unchanged. If I pressed the shape into a bed of concrete, then a symmetry would be any change in its orientation I could make that would allow me to stick it back into the impression I made in the concrete. For dihedral groups, we limit the symmetries we can apply to two types: rotations and flips.
Rotations are defined by rotating the regular n-gon by 360/n degrees. For a square, that’s a 90° rotation as seen in Fig. 1.4.3, for pentagons it’s 72°, etc. Flips are, well, flipping the regular n-gon across a chosen axis. An example of a flip is shown in Fig. 1.4.4. Rotations and flips are denoted by r and f respectively.

But there are certainly many more things we could do to the square than a 90° rotation and a flip. For example, what if we did two rotations? Or a rotation and then a flip? These are all valid symmetries of the square, and so are part of its dihedral group. If we wanted to algebraically denote two rotations, we’d write r2, or if we wanted a rotation followed by a flip, we’d write rf. The set of all these possible orientations plus the operation of combining actions is called a dihedral group. There’s a unique dihedral group for each regular n-gon, denoted by Dn. So the group of symmetries of a square is D4, or “dihedral group degree 4”.
You might notice that every element in Dn is some product of r and f. When this happens, we say that r and f are generators of the group: every element in the group can be expressed as their products. This is denoted with 〈r,f〉. The generators of a group are essential to drawing a group’s Cayley graph.
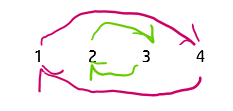
Everything we’ve talked about has been in the shallow end of the group theory pool, and groups can get very complex very quickly. One method of visualising groups at the introductory level are Cayley graphs. Cayley graphs are networks of nodes connected by edges. The nodes are elements in the group, and the edges are the generators. The basic principle is that you can start from any element in the group and apply some sequence of the generators to reach any other element in the group. If you make each element a dot, and draw a line for each generator you use, then you can create a network that completely represents the group. Fig. 1.4.5 shows a crudely drawn Cayley graph for the group D3, the dihedral group for an equilateral triangle.

Hopefully that graph is fairly self-explanatory. If you rotate a triangle 120° three times, it will get back to its original position, hence the cycle of three red arrows. Whereas if you flip a triangle along an axis twice, it returns to the original position, i.e. the identity, which is why the green lines don’t have arrows. (Sidebar, the order of an element is the minimal number of times you need to apply it to itself to produce the identity. In this case, the order of r is 3, and order of f is 2).
Note that a group can have multiple different generators, and thus multiple different Cayley graphs. The graphs can also change depending on how you draw them, which makes Cayley graph suck pretty hard for doing proper group theory. However, they are helpful tools to gain intuition for some aspects of the subject otherwise.
If you wanted to go really in-depth, you could say that the group presentation for Fig. 1.4.5 is D3 = 〈r , f | r3, f2, (rf)2〉. Where the symbols on the left of the vertical bar are the chosen generators, and the symbols on the right of the bar are the minimal set of relations.
1.5 Cyclic Groups
Some things should come a lot easier now that we have some basic concepts and notation explained. As such, cyclic groups should not take us as long.
Cyclic groups are groups that are generated by one element. Some examples of Cyclic groups you might be familiar with are modular arithmetic and rotations. As we’ve just looked at rotations, let’s go over those.
If you had a 120° rotation on a triangle, r, then applying it once would give you a triangle rotated by 120°, and r2 would give you a 240° rotation. For r3, it gives a 360° rotation, which is equivalent to no rotation at all. Thus r4 is equivalent to r, and so on, until r6 which starts over again. What we have here is a cycle of elements generated by one element, r. Rotations are trivially closed, and associative, the identity is clear, and r-1 can be generated as rn-1. Thus, this collection of elements forms a group under the operation of combining rotations. This holds generally for any cycle generated by one element which repeats periodically. These are what are called cyclic groups, denoted by Cn where n is the order of the generator.
For those curious, try drawing the Cayley graph of a cyclic group.
1.6 Symmetric Groups
Symmetric groups are a little different to what we’ve looked at so far. They have all either been talked about geometrically as rotations and actions on a shape, or algebraically. Symmetric groups give us something new to chew on.
A permutation is when you take a set of elements and rearrange the order they appear in without repetition. To talk about permutations, it’s nice to have a ready notation. The way that I like to represent permutations is with a matrix. Let’s use a set of 4 as an example. Take Fig. 1.6.1 as a permutation on a set of 4 objects where 1 and 4 are swapped, and 2 and 3 are swapped. This permutation can be written as the matrix “1,2,3,4/4,3,2,1” (excuse my notation, edublog is allergic to math notation) where the number on the top gets swapped with the number on the bottom.
Of course, what we want to see is if these permutations form a group. Closure is pretty obvious, if I do two permutations, I’m going to get another permutation. The identity is the permutation “1,2,3,4/1,2,3,4,” and the inverse of a permutation “1,2,3,4/4,3,2,1″ is the permutation “4,3,2,1/1,2,3,4″. Associativity is a bit harder to prove, and ultimately boils down to function composition, which I won’t pretend to understand or go into. Regardless, these groups are called symmetric groups and are denoted by Sn, where n is the number of objects the permutation is acting on.
Symmetric groups actually have a really interesting property known as Cayley’s theorem, which states that every group is equal to some subset of a symmetric group. I won’t prove it here, but intuitively, if you think of a group acting on some shape, and number the vertices of that shape, then after some action you can think of the vertices being in a different “order” than they were in before, analogous to a permutation.
2.1 Result Progress
That was definitely a lot, but I hope you have a better sense of what the world of groups is like. We now enter the last section, where I report on the progress I’ve made in creating a result.
My mind has been going into two directions recently. My first idea is to pursue groups as matrices. You got a taste of how that may play out in 1.6. The general idea is to work with the matrices of symmetry groups and treat them as matrices instead of groups. Specifically, I know that certain matrices act as transformations on a vector space, so it might yield something to see how groups affect those spaces. Something I would definitely look into further would be how to represent other groups (not just symmetrical ones) as matrices. According to the wisdom of my mentor, apparently the consequences of viewing groups as matrices is a legitimate field which already exists, called representation theory. So all in all, that idea is promising.
My second idea comes in-part from preliminary research. When I was first scouting out group theory as a possible In-Depth topic, I came across things called Lie groups, which were described as “differentiable manifolds”. Exciting. I left those alone for obvious reasons until I started doing some group theory and thinking about the subject more. The idea of a binary operation (of which all groups have one) was striking. The two inputs-one output structure reminded me a lot of functions, except this time in three dimensions, which is a perfect setup for making a surface, or a differentiable manifold. This wouldn’t work for all groups though. For all the groups we’ve discussed here, they wouldn’t form a surface, but instead a loose collection of points. This is caused by the fact that all of these groups are discrete. Take D3. There are three possible rotations, but nothing in-between those rotations to make that smooth, differentiable surface. So if this group-generated surface were to work, it would require an infinitely large group whose elements are infinitely “close together”. Luckily, I already know a couple of groups like this. For example, the rotational symmetries of a circle (you can rotate the circle by any real number angle, and it makes a valid symmetry) or the displacement symmetries of an infinitely long line.
Then, on the meeting I had with my mentor, we were going through some of his books looking for applications of group theory and we stumbled onto the Lie group section, which stated that Lie group elements are infinitesimally close together. Needless to say, this path looks promising, and is probably the one I’m more interested in pursuing.
This does have a substantial issue however. That being, I don’t know any other groups meeting the surface criteria other than the two above. I don’t expect the structure of those two groups to be very interesting anyway, so it very much limits the scope of what I can study. I’m hoping that as I progress through the subject, I’ll become familiar with more surface-generating groups, or schemes to produce them.
Overall, I’ve paid most of my attention to learning Galois theory and my other exploits not in group theory, though I’ve kept my result in the back of my mind.
If you’re interested in learning more, I’d recommend Matthew Macauley’s lectures on the topic:
https://youtube.com/playlist?list=PLwV-9DG53NDxU337smpTwm6sef4x-SCLv
Join me next time to (probably) learn about quotient groups and direct products. They are certainly more of a doozy, but provide a rich substructure to groups in return.
.