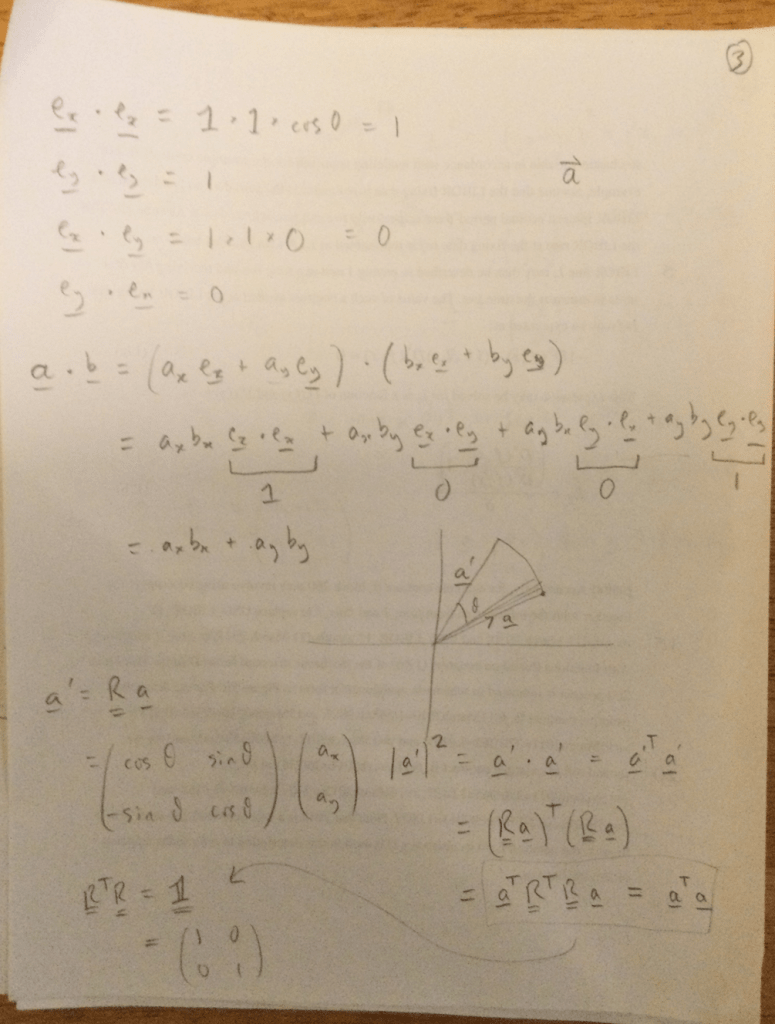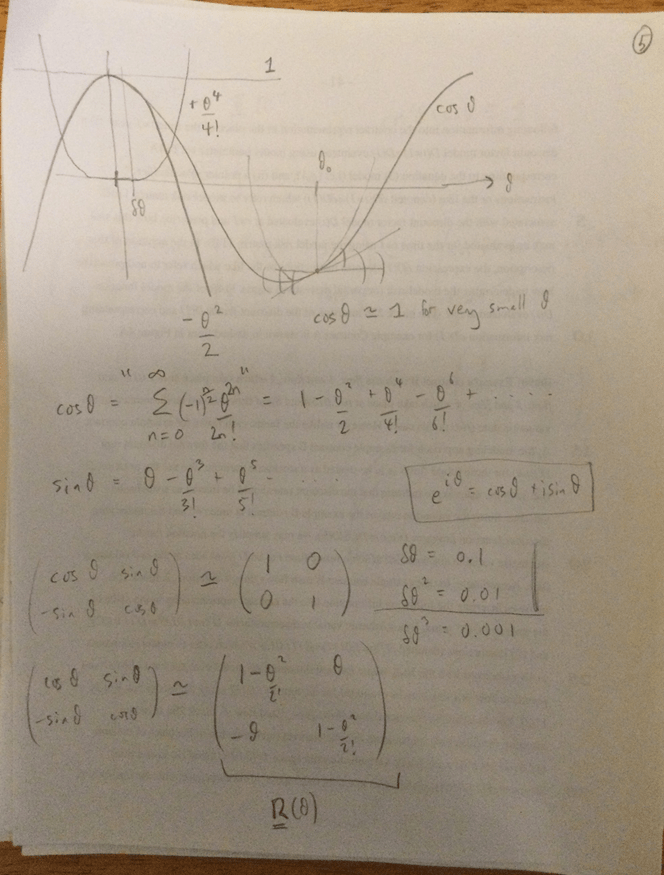Log Series
The second installment in my log series is currently under construction and behind schedule, though it should contain much more information than the first installment. Nevertheless, the link below will direct you to the incomplete version of the post, which will be replaced with the complete version during the weekend.
https://mygleneagle.sd43.bc.ca/pavelv2021/2022/04/01/in-depth-2022-group-theory-captains-log-2/
Good and Bad Things About Mentoring
I have encountered two large difficulties over the course of our meetings. The first problem we have largely solved, but was an interesting challenged we faced. This problem was that we couldn’t find too much to talk about during each session. I would go in with hopefully a handful of questions, and we would work through them together to reach a conclusion. While this was valuable, I felt like this mentorship opportunity could be used for something more interesting than glorified homework help. The way we fixed this was by tackling a much harder problem to solve than “explain this theorem”. Instead, we would pick some topic which was largely out of my usual scope (like Lie groups or Representation Theory) and we would discuss this together.
Those two situations seem very similar, but the quality of our discussions were much better in the latter. The principal difference was that we could discuss more conceptual ideas that challenged what my notions of the subject were. An example was our dive into Lie groups. Having only dealt with finite groups up to this point, I felt it was more enriching to discuss what it would mean to have a group where all the elements are infinitely close together and unending in number, and how you might go about doing that. It was a topic like this where I was expanding my understanding of the subject which I felt was better to have the guidance of a mentor, instead of the detail-specific homework-like questions, which I could probably do on my own anyways.
We have thus changed the nature of our meetings to these more open-ended type discussions. This, however, creates its own problems. Principally, that we have too many interesting things to talk about that we haven’t had enough time in our sessions. Our sessions have averaged 1-1.5 hours, but it’s never finished of our own volition, always because of outside influence. It really feels like we could talk about these things for hours, and a session always finishes with a rushed and slightly unsatisfactory explanation of our topic. This is, funnily enough, the exact opposite to the problem we had before.
I Will Improve
Again, our biggest problem is that we haven’t had enough time to adequately explore the topic. I can improve this situation by communicating this issue and my desire to change it to my mentor. We’ll probably discuss this on our Discord server and find a larger time slot that works for him (as I am free basically always).
Another thing that we (mostly I) could improve on is giving my mentor advance notice of what we’ll be talking about. Our discussions have been largely impromptu so far, and so he hasn’t had any time to prepare a response or interesting directions to take it. Given that he is no human computer, it would probably be beneficial if I gave him some time to prepare these things beforehand by telling him what I’m interested in. Amazingly, I’ve already done this for our next meeting, and we’ve decided to talk more about Representation Theory, which he’s always alluded to, but I’ve never fully explored.
General Progress Report
My progress is best represented through my log series, where I feel freer to go into juicy mathematical detail.
I have learned quite a bit throughout this project. The types of groups, the types of subsets in groups, group mappings, and various theorems. One of the most notable things I’ve gained is an answer to one of my main questions/goals of this In-Depth project. That question being why groups are important and everywhere? Principally, why they’re of such high importance in particle physics. That is what I got answered, courtesy of my mentor.
Of course, I am not close with the details, and I don’t really understand it (this is multiple semesters’ worth of material), but I have a much better idea than when I started. Essentially, there are physical theories that are invariant under certain transformations. For example, many classical theories have the idea that if you did the experiment in one location, and then did it in another location, with everything else being equal, they should be the same. I.e., simply changing the coordinates aren’t going to do anything, or in other words, the theory is invariant under translations.
Now in quantum mechanics, you more or less represent the system using a wavefunction, and what you want is this wavefunction to be invariant under rotations. Thus, the wavefunction has a symmetry kind of similar to an n-gon, and can be represented as a group. In the case of the wavefunctions, its symmetries are the myriad rotations of 3-dimensional space, which is expressed using a Lie group. This Lie group is infinitely large with elements all infinitesimally close together. This corresponds to the fact that there are an infinite number of real number angles with which you can rotate 3-space, and these are all infinitesimally close together. Anyways, the symmetry of the wavefunction, or the system, can be expressed using a Lie group, and the theory as a whole has a larger symmetry that encompasses a large number of different wavefunctions. This larger symmetry is the direct product of a couple Lie groups. The kicker here, is that for some arcane reason, the particles that we observe and which the theory says are allowed to exist, correspond directly to the generators of that direct product group. This I find to be very, very baffling. That there should be some incredibly deep connection between the study of symmetry, and the things that we’re made of.
That connection was also not disappointing at all. I had no idea what to expect from the importance of Lie groups in the standard model, and I thought that they might just be some computational tricks, but no. The very existence of the particles themselves are the generators of a group. That’s pretty insane, and encourages me to learn more about these things to understand that connection better.
Let’s not even get into how they characterized the Lie group of rotation matrices, which I thought was really clever and cool. Essentially, the rotation matrix is filled with a bunch of trig functions of the angle you’re rotating by. The thing about the Lie group though, is that you’re worried about angles that start off as infinitesimal and increase infinitesimally. So you can take the Taylor expansion of the trig function, and include however many terms are needed to get an accurate estimate for your angle. Now all of a sudden, your rotation matrix is filled with polynomials instead of pesky trig functions.
The following are the things my mentor wrote down as we talked about Lie groups. Most of it is linear algebra. The reason for this is that my mentor has very in-depth explanations, and the applications of Lie groups to rotations of space have to do with creating a Lie group with rotation matrices. Given, however, that I know very little linear algebra, many preliminary ideas he chooses to discuss.